Consider a modification of the rod cutting problem information

Home » modification » Consider a modification of the rod cutting problem information

Your Consider a modification of the rod cutting problem images are available. Consider a modification of the rod cutting problem are a topic that is being searched for and liked by netizens today. You can Get the Consider a modification of the rod cutting problem files here. Get all free vectors.

If you’re searching for consider a modification of the rod cutting problem images information linked to the consider a modification of the rod cutting problem keyword, you have come to the right blog. Our website frequently provides you with suggestions for seeking the highest quality video and image content, please kindly surf and find more enlightening video articles and images that fit your interests.

Consider A Modification Of The Rod Cutting Problem. Thus The Revenue Is Now The Sum Of All Pis Minus The Costs Of Cuts. B Explain how the rod-cutting problem described in class can still be solved by dy-namic programming even if cuts now cost 1 each. The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut. See the Code for better explanation.

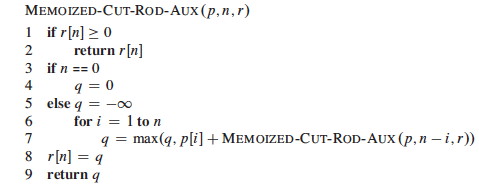Ics 311 12 Dynamic Programming From algoparc.ics.hawaii.edu

Bank of america third party authorization form for modification 45 raptor magazine modification Ak 47 charging handle modification Ancient body modification

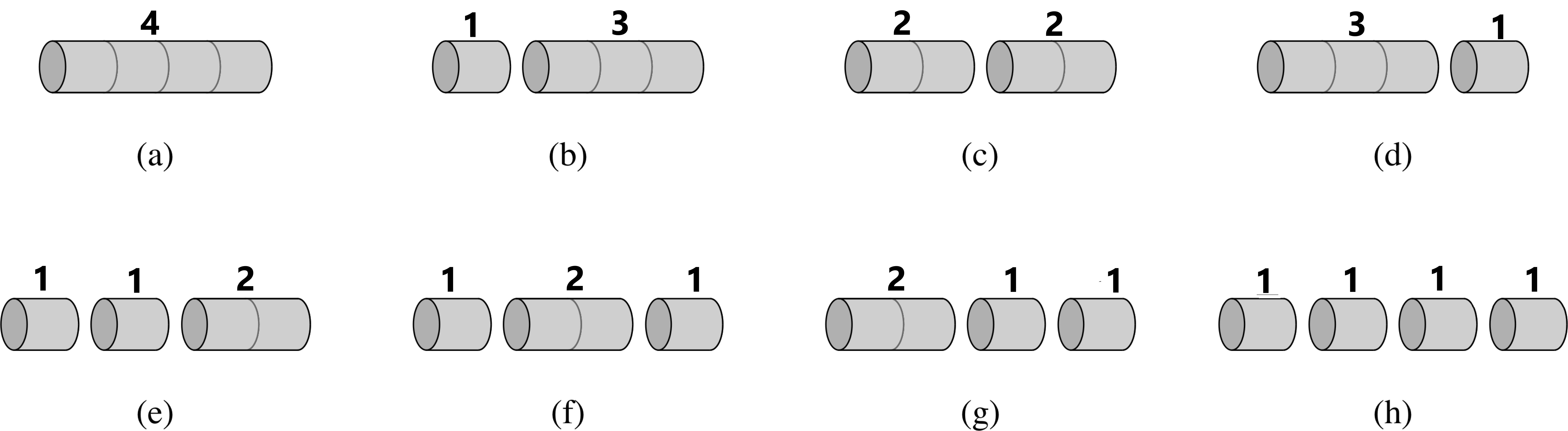
Consider a modification of the rod-cutting problem in which in addition to a price p_i for each rod each cut incurs a fixed cost of c. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. A piece of size 3 there is no further demand for rods of size 3 so we dont want to cut any more of that size. Give a dynamic-programming algorithm to solve this modi ed problem. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. So the Rod Cutting problem has both properties see this and this of a dynamic.

If len.

If len. Solution for LRS Exercise 151-3 Rod Cutting Problem Consider a modification of the rod-cutting prolem in which in addition to a price pi for each rod each cut. Ans pk for i range1 k. Find correct step-by-step solutions for ALL your homework for FREE. B Explain how the rod-cutting problem described in class can still be solved by dy-namic programming even if cuts now cost 1 each. In class we assumed cuts were free Here is the pseudocode for the original solution where the cuts were free.

Source: algoparc.ics.hawaii.edu

A piece of size 3 there is no further demand for rods of size 3 so we dont want to cut any more of that size. See the Code for better explanation. In Addition To A Price Pi For Each Rod Each Cut Incurs A Fixed Cost Of C. Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c. B Explain how the rod-cutting problem described in class can still be solved by dy-namic programming even if cuts now cost 1 each.

Source: slideplayer.com

Consider a modification of the rod-cutting problem in which in addition to a price pi for each rod each cut incurs a fixed cost of c. I maxprice maxoftwo. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. Show the algorithms. Fundamental Algorithms CSCI-GA1170-001 Summer 2016 Homework 9 Problem 1 CLRS 151-3.

Source: iq.opengenus.org

In Addition To A Price Pi For Each Rod Each Cut Incurs A Fixed Cost Of C. Coz if the stick doesnt have to cut at all the markings and the price is independent of the length of the chopped wood then the minimum price would be L for chopping just once. Exercise 151-3 page 370 Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c. It feels as if something is missing from this problem may be a constraint. Include include int maxoftwo int a int b if a b return a.

Source: slideplayer.com

In class we assumed cuts were free Here is the pseudocode for the original solution where the cuts were free. The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut. AConsider a variant of the rod-cutting problem where we can only sell a piece of size i once thus once we cut eg. If len. Int rodcut int prices int len int maxprice INTMIN.

Source: slideplayer.com

Give a dynamic-programming algorithm to solve this modified problem. Rather than adding two r values eg r 2 and r k 2 we can add a p value and an r value eg p 2 and r k 2 This approach determines which first cut ie p i gives the best revenue. The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. Give a dynamic-programming algorithm to solve this modified problem.

Source: medium.com

Consider a modification of the rod-cutting problem in which in addition to a price pi for each rod each cut incurs a fixed cost of c. I len. Note that in this setting the best solution might wind up with a nal piece. I maxprice maxoftwo. In class we assumed cuts were free Here is the pseudocode for the original solution where the cuts were free.

Source: slideplayer.com

Include include int maxoftwo int a int b if a b return a. Int rodcut int prices int len int maxprice INTMIN. I len. On2 On3 Onlogn O2n. In Addition To A Price Pi For Each Rod Each Cut Incurs A Fixed Cost Of C.

Source: algoparc.ics.hawaii.edu

Instead of solving the sub problems repeatedly we can store the results of it in an array and use it further rather than solving it again. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the v cuts. Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c. Since same suproblems are called again this problem has Overlapping Subprolems property. Generally DP problems have a constraint under which you have to minimise or maximise a quantity.

Source: slideplayer.com

The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut. A piece of size 3 there is no further demand for rods of size 3 so we dont want to cut any more of that size. Find correct step-by-step solutions for ALL your homework for FREE. Int rodcut int prices int len int maxprice INTMIN. Give a dynamic-programming algorithm to solve this modified problem.

Source: algoparc.ics.hawaii.edu

The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut. Consider a modi cation of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a xed cost of c. I maxprice maxoftwo. Data Structures and Algorithms Objective type Questions and Answers. See the Code for better explanation.

Source: algoparc.ics.hawaii.edu

Give a dynamic-programming algorithm to solve this modified problem. 1 point Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of cThe revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. Note that in this setting the best solution might wind up with a nal piece.

Source: slideplayer.com

Exercise 151-3 page 370 Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the v cuts. Rod Cutting 20 points. R 0 n 1 for k in range1 n 1. Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c.

Source: slideplayer.com

The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. I len. Give a dynamic-programming algorithm to solve this modified problem. Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c.

Source: slideplayer.com

Int rodcut int prices int len int maxprice INTMIN. The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut. Question 1 2 Points Rod-cutting Problem Consider A Modification Of The Rod-cutting Problem. On2 On3 Onlogn O2n. Int rodcut int prices int len int maxprice INTMIN.

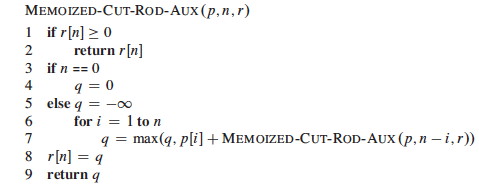Source: algoparc.ics.hawaii.edu

Consider a modification of the rod-cutting problem in which in addition to a price pi for each rod each cut incurs a fixed cost of c. Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c. Rod Cutting Problem Overlapping Sub problems. See the Code for better explanation. The revenue associated with a solution is now the sum of prices of the peices minus the cost of making the cut.

Source: techiedelight.com

Question 1 2 Points Rod-cutting Problem Consider A Modification Of The Rod-cutting Problem. R k max p k r 1 r k 1 r 2 r k 2 r k 1 r 1 Better solution. Generally DP problems have a constraint under which you have to minimise or maximise a quantity. Rod Cutting 20 points. I maxprice maxoftwo.

Source: algoparc.ics.hawaii.edu

Coz if the stick doesnt have to cut at all the markings and the price is independent of the length of the chopped wood then the minimum price would be L for chopping just once. A piece of size 3 there is no further demand for rods of size 3 so we dont want to cut any more of that size. Note that in this setting the best solution might wind up with a nal piece. Give a dynamic-programming algorithm to solve this modified problem. Consider a modification of the rod-cutting problem in which in addition to a price p i for each rod each cut incurs a fixed cost of c.

Source: slideplayer.com

In class we assumed cuts were free Here is the pseudocode for the original solution where the cuts were free. On2 On3 Onlogn O2n. A Now Instead Of Rn Max Pn Pı Rn-1P2 Rn-2 Pn-1 rı The Revenue Should Be The. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. Instead of solving the sub problems repeatedly we can store the results of it in an array and use it further rather than solving it again.

This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.

If you find this site value, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title consider a modification of the rod cutting problem by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.